What is Variational Inference 🌱

• Firstly, the word “variational” is a fancy word for optimization-based formulas

The Challenge

Direct inference on our distribution \(P\) can be intractable

• We can approximate inference on \(P\) by projecting it to a family of distributions \(Q\) and perform inference on this new distribution family
• We select the projection that minimizes the KL divergence \(D_{K L}(Q \| P)=\int_{-\infty}^{\infty} q(\theta) \log \frac{q(\theta)}{p(\theta , X)} d \theta\)

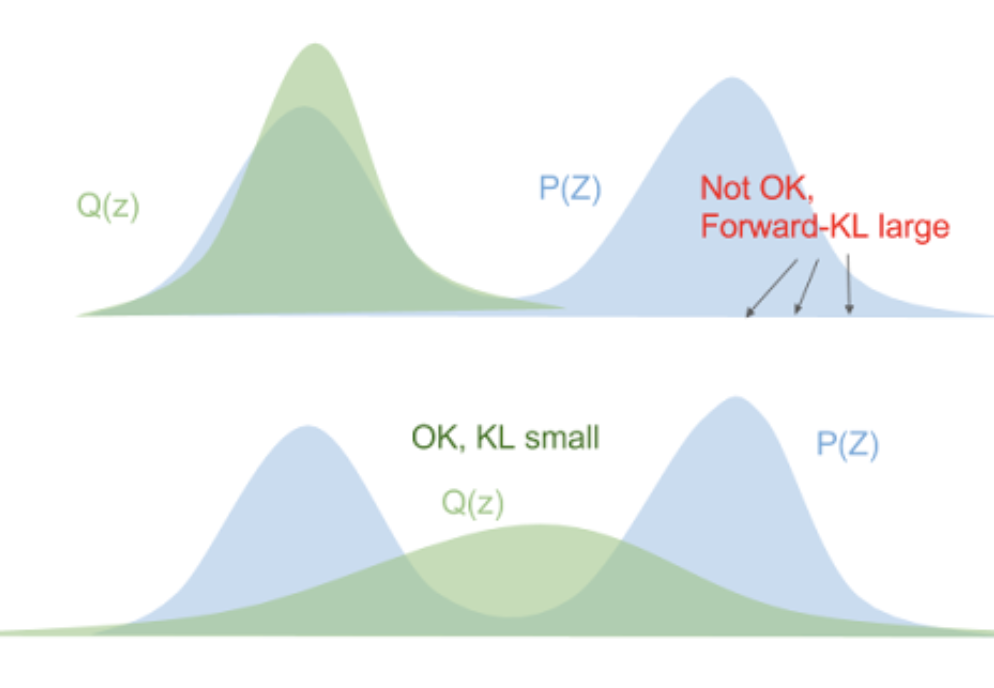
KL Divergence

\(D_{KL}(P|Q) = \sum_i p(x_i)\log \frac{p(x_i)}{q(x_i)}\)	\(D_{KL}(Q|P) = \sum_iq(x_i)\log \frac{q(x_i)}{p(x_i)}\)

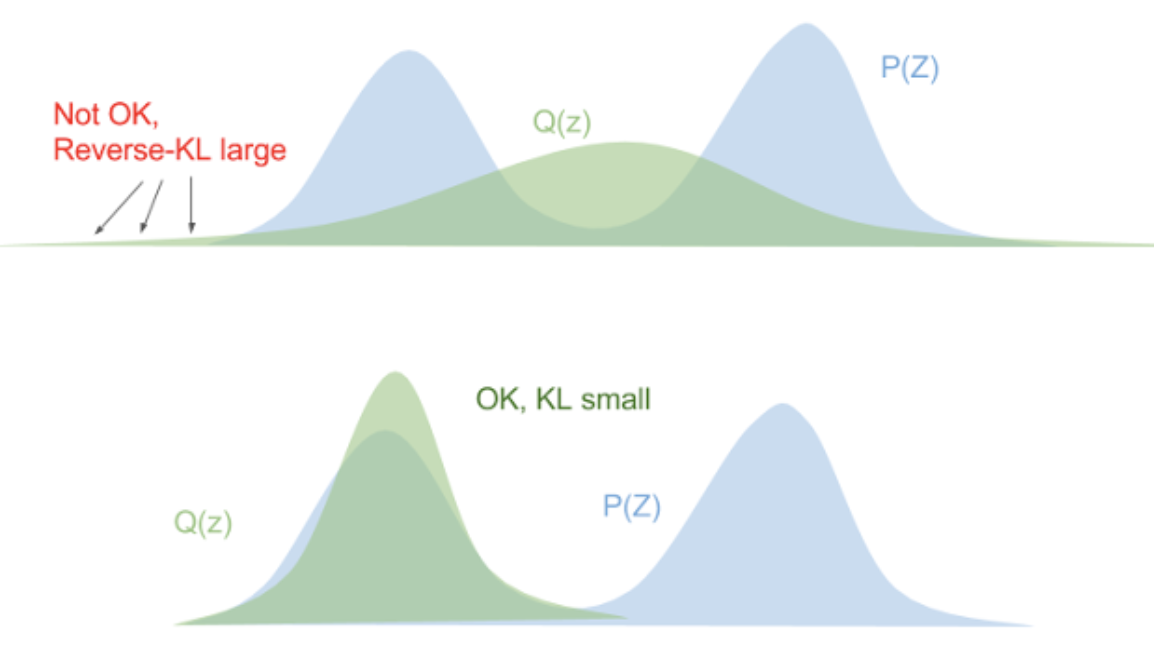• We try to minimize the reverse KL since it has the nice tendency to make our \(Q\) distribution match at least one of the modes of \(P\), which is the best we could hope for with the shape of our approximation.
• However, we can’t actually minimize this directly since it depends on the intractable distribution \(p\) so we actually maximize the evidence lower bound (ELBO) (check this link for the math)

Mean Field Approximation

We assume that the \(Q\) distribution partitions our variables of interest into independent parts:

Suppose that we are interested in finding the joint probability \(p(\beta,\omega,z)\), then based on our assumption of the distribution \(Q\):

Solving for the optimal \(q_j(\theta_j)\) yields that (check this link for the math):

where \(E_{m | m \neq j}[\log p(\theta, X)]=\int_{\theta_{m | m \neq j}}\left[\prod_{i \neq j} q_{i}\left(\theta_{i}\right)\right] \log p(\theta, X) d \theta_{1} \ldots, d \theta_{j-1}, d \theta_{j+1}, \ldots, d \theta_{n}\) is the expectation across all variables except for \(j\).

Now the algorithm goes:

1. For each \(q_j\) use the above equation to minimize the overall KL divergence by updating \(q_j(\theta_j)\) holding all the others constant.
2. Repeat until convergence