What is the Wake Sleep Algorithm 🌱

Hemholtz Machine

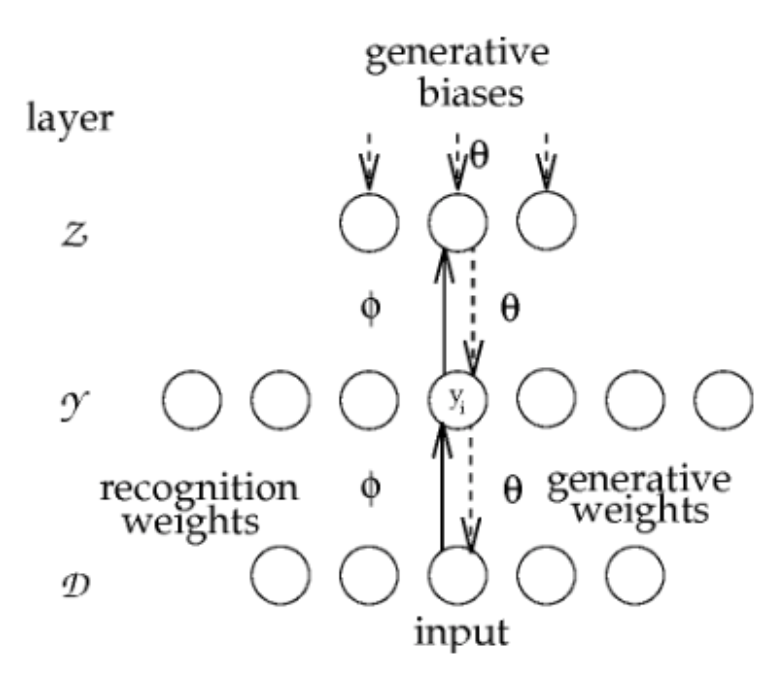
We have two networks:

1. Recognition network with weights $\varphi$ converts input data $x$ into latent representations used in successive hidden states $z$.
2. Generative network reconstructs data from the latent states using weights $\theta$.

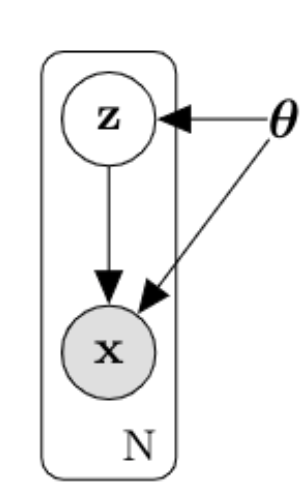
The Hemholtz machine tries to learn $\varphi$ and $\theta$ such that $q_{\varphi }(z\mid x)\approx p_{\theta }(z\mid x)\propto p_{\theta }(z,x)$

• $q_{\varphi }(z\mid x)$ is the variational distribution approximating the posterior $p_{\theta }(z\mid x)$

Wake Phase

1. Feed $x^{\left(i\right)}$ into the recognition network to get ${\mu }_{\varphi }\left(x^{\left(i\right)}\right)$ and ${\Sigma }_{\varphi }\left(x^{\left(i\right)}\right)$
2. Draw $L$ samples $z_1^{\left(i\right)},\dots ,z_L^{\left(i\right)}\sim q_{\varphi }(z\mid x^{\left(i\right)})=N(z;{\mu }_{\varphi }\left(x^{\left(i\right)}\right),{\Sigma }_{\varphi }\left(x^{\left(i\right)}\right))$
3. For each $l\in \left[L\right],$ feed $z_l^{\left(i\right)}$ into the generative network to get $f_{\theta }\left(z_l^{\left(i\right)}\right)$ for the likelihood $p_{\theta }(x\mid z_l^{\left(i\right)})=$ Bernoulli(x; $f_{\theta }\left(z_l^{\left(i\right)}\right))$
4. Optimize for ${max}_{\theta }{\sum }_{i=1}^N\frac{1}{L}{\sum }_{l=1}^L\log p_{\theta }(x^{\left(i\right)}\mid z_l^{\left(i\right)})$

• Simulate latent state by feeding input data to recognition network and maximize how well the generator’s probabilities for the hidden state fit the actual data.

Sleep Phase

1. Draw $z^l\sim N(0,I)$
2. Sample $x^l$ from the generative network $p_{\theta }(x\mid z^l)=Bernoulli\left(f_{\theta }\left(z^l\right)\right)$
3. Feed $x^l$ into the recognition network to get $\mu \left(x^l\right)$ and $\Sigma \left(x^l\right)$
4. Compute $q_{\varphi }(z^l\mid x^l)=N(z^l;\mu \left(x^l\right),\Sigma \left(x^l\right))$
5. Optimize ${max}_{\varphi }\frac{1}{L}{\sum }_{l=1}^L\log q_{\varphi }(z^l\mid x^l)$

• Simulate random $x$ data by following the generator. Then maximize the probability that the recognition network suggests the correct latent states given the simulated $x$.