What is the Hidden Markov Model 🌱

The Hidden Markov Model (HMM) is a time series model that assumes the ground truth is made up of observed variables that we see o1,…,ot and hidden variables s1,…,st that we never see but determine the values we observe. There are two main assumptions with the HMM:

1. P(st∣st−1,st−2,…,s1)=P(st∣st−1)
2. P(ot∣ot−1,ot−2,…,o1,st,st−1,…,s1)=P(st∣st−1)=P(ot∣st)

• The first assumption means that the next hidden state is only dependent on the directly previous hidden state and none of the other past hidden states.
• The second assumption means that the observation at a certain time point is only dependent on the hidden state at that time point.

Here is a visualization of what the HMM looks like where xt are the hidden states and yt are the observed values.

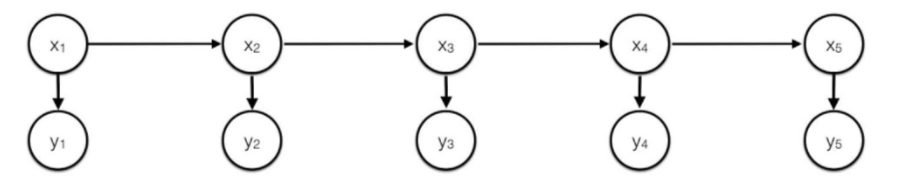
There are 3 main problems we can solve with the HMM model, where A is a n×n matrix of transition probabilities like P(st∣st−1), B is a n×v matrix of emission probabilities like P(ot∣st), O is the sequence of observed values, and S is the sequence of states. This model assumes that transition and emission probabilities are constant over time (but this can be generalized by having A as a T×n×n tensor).

1. Compute P(O∣A,B)
2. Compute S∗=argmaxSP(S,O∣A,B)
3. Compute $A^,B^ = \text{argmax}_{A,B} P(O \mid A,B)$