What is the Dirichlet Process 🌱

Last updated on August 10, 2020

A Dirichlet distribution is a distribution over probability vectors based on some parameters. What if we want those parameters to be random?

A Dirichlet Process is basically a distribution over distributions of parameters

Dirichlet Distribution

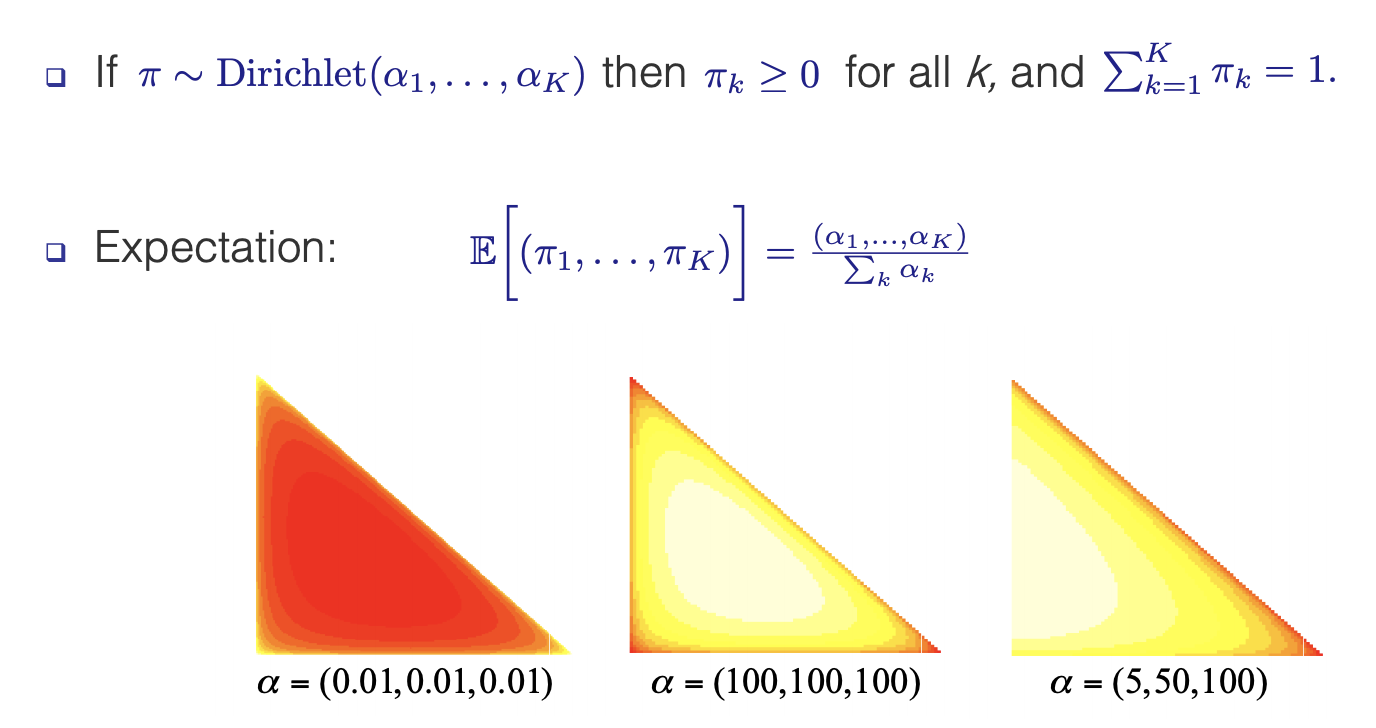
A Dirichlet distribution is often used to probabilistically categorize events among several categories. Suppose that weather events take a Dirichlet distribution. We might then think that tomorrow’s weather has probability of being sunny equal to 0.25, probability of rain equal to 0.5, and probability of snow equal to 0.25. Collecting these values in a vector creates a vector of probabilities.
The Dirichlet distribution is a distribution over positive vectors that sum to one (probabilities).
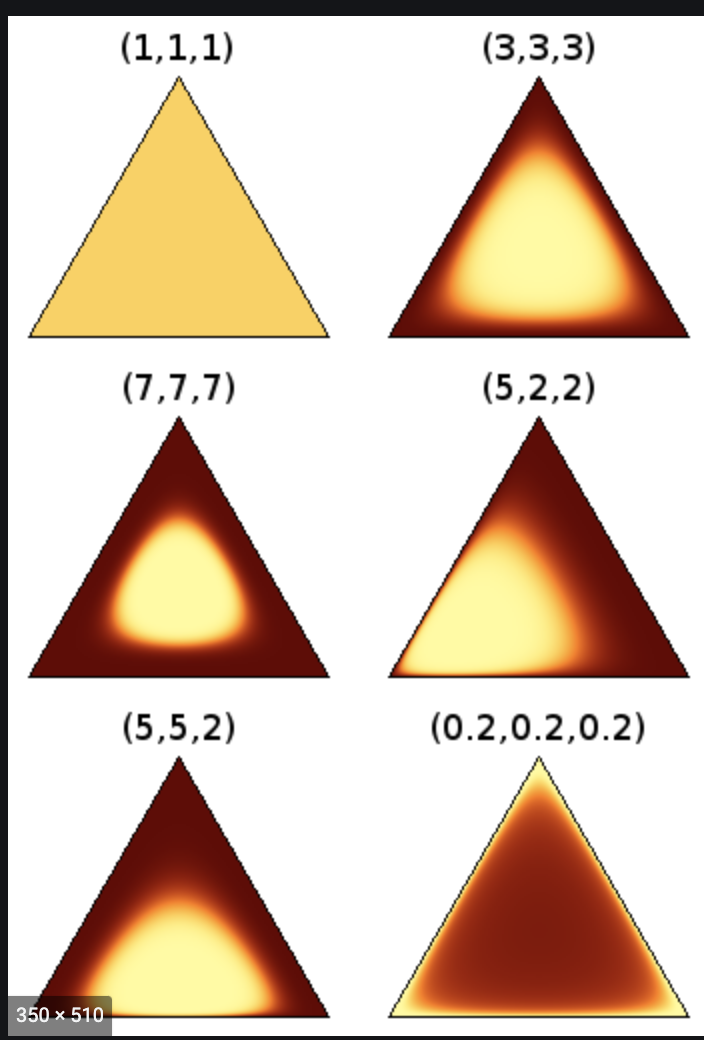
Below shows what Dirichlet distributions with different parameters look like:

Relation to Beta Distribution

A beta distribution is often used to describe a distribution of probabilities of dichotomous events, so it’s restricted to the unit interval.
For example, for a Bernoulli trial, there is only a parameter $θ$ describing the probability of a “success.” Often we think of $θ$ as being fixed, but if we are uncertain about the “true” value of $θ$ , we could think about a distribution of all possible $θ$ s, with a larger likelihood for those we consider more plausible, so perhaps $θ \sim B (α, β)$ , where $α > β$ concentrates more of the mass near 1 and $β > α$ concentrates more of the mass near 0.
Extending the beta distribution into three or more categories gives us the Dirichlet distribution

Defining the Dirichlet Process

G \sim D P (α, H)

Definition 1

Let $H$ be a distribution on some space $Ω$ (e.g. a Gaussian distribution on the real line) with the following known:

π \sim lim_{K \to \infty} Dirichlet (\frac{α}{K} \dots, \frac{α}{K})

for k = 1, \dots \infty let θ_{k} \sim H

Then

G (θ) = \sum_{k = 1}^{\infty} π_{k} δ_{θ_{k}} (θ) is an infinite distribution over H and G \sim D P (α, H)

where $δ_{θ_{k}}$ is the indicator which is zero everywhere except for $δ_{θ_{k}} (θ_{k}) = 1$ $

Definition 2

A Dirichlet process is the unique distribution over probability distributions on some space $Ω$ , such that for any finite partition $A_{1}, \dots, A_{K}$ of $Ω$ . So if $P \sim D P (α, H)$ then:

(P (A_{1}), \dots, P (A_{K})) \sim Dirichlet (α H (A_{1}), \dots, α H (A_{K}))

Relating to the Chinese Restaurant Process

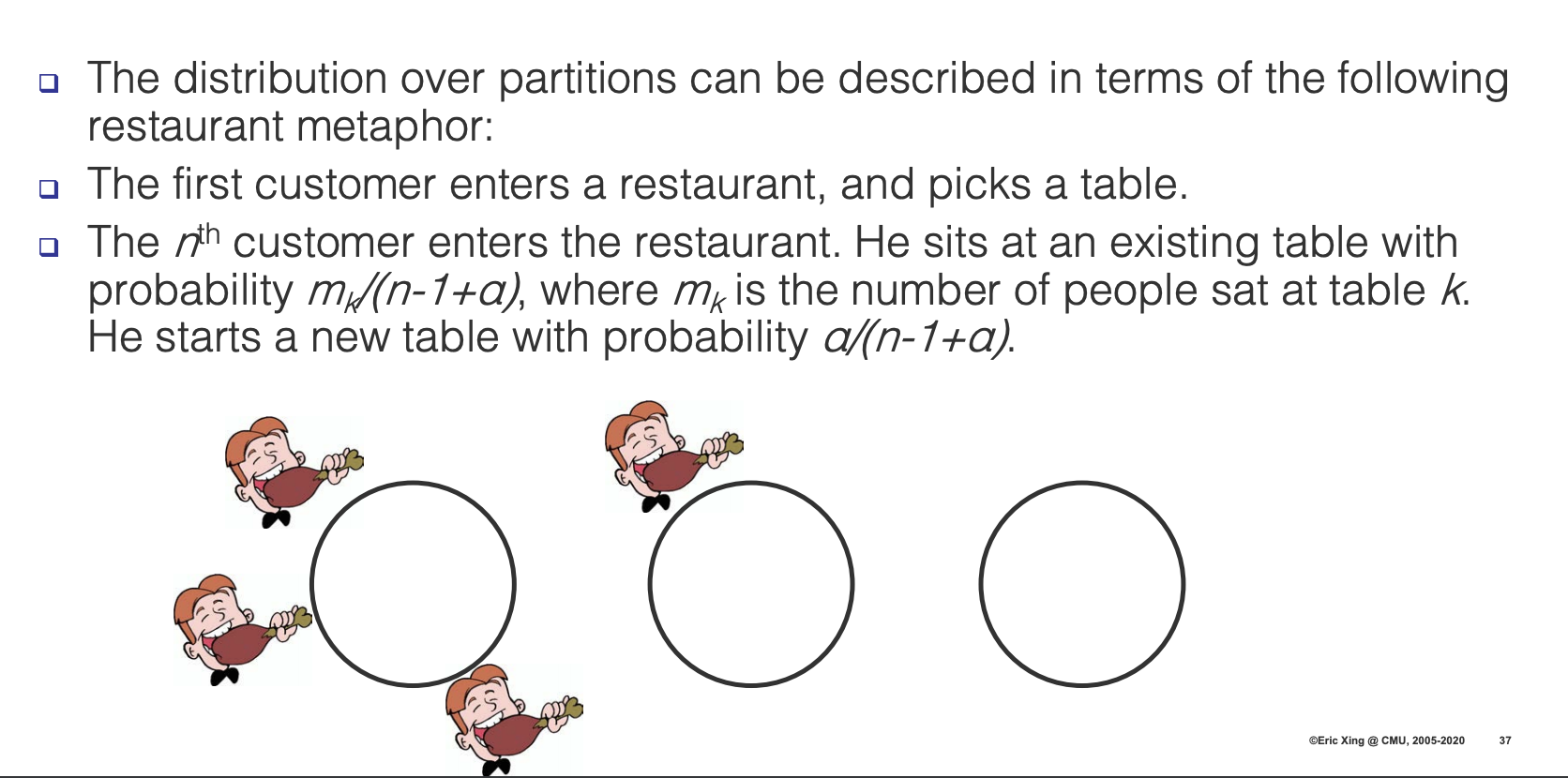
Each partition $A_{1}, \dots, A_{K}$ represents a table at the restaurant
$P (A_{i})$ is the probability mass of customers on table $i$ (e.g. $n_{i} / N$ )
$H (A_{i})$ is a draw from the base measure $H$ for the corresponding table $A_{i}$ . This could act as the label for a table.

This could also be explained with the Polya Urn Process which is basically identical except that each $A_{i}$ represents a color, with $H (A_{i})$ as a base measure from the color and $P (A_{i})$ as the probability mass of that specific color

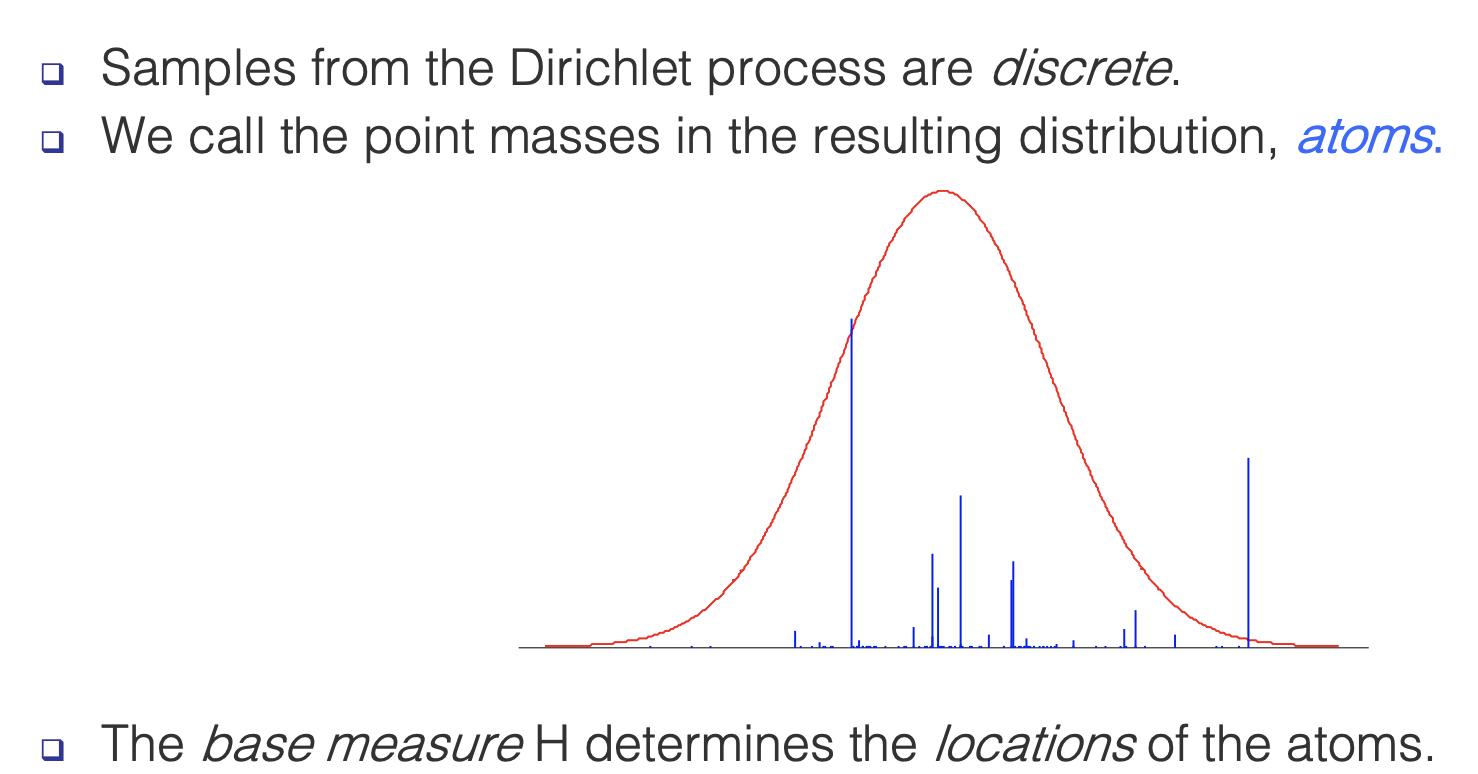
Sampling from the DP


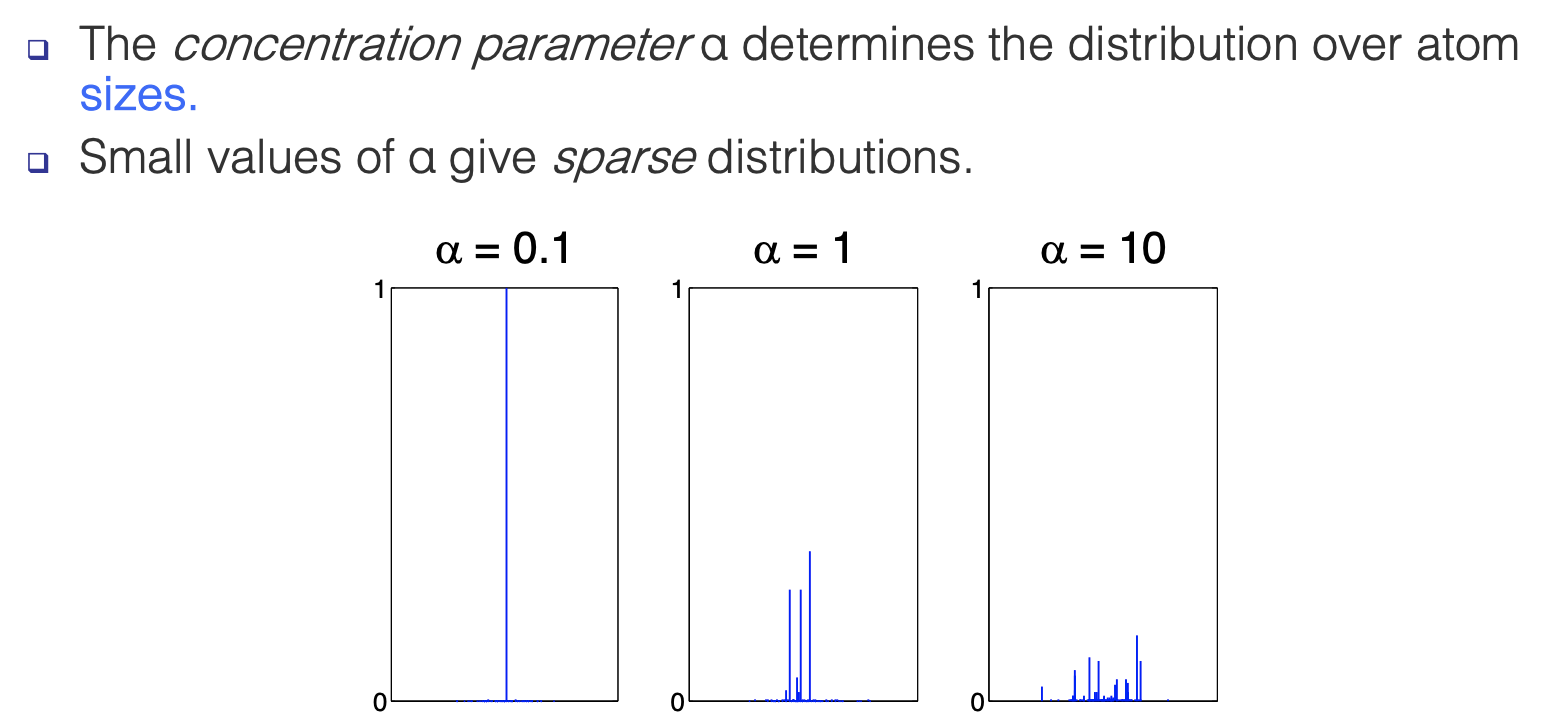
The base measure $H$ does not influence the probability of a point joining that atom/class, it only influences the locations of the atoms (the value of the class) as shown in the graph above.	These properties of alpha are true because this means that a new value is less likely to take on a new class value with a small alpha (see predictive distribution below)

Predictive Distribution

A new data point can either join an existing cluster, or start a new cluster. What is the predictive distribution for a new data point?

Hierarchical Dirichlet Process/Chinese restaurant franchise

10-708 Lecture Notes

Notes mentioning this note

There are no notes linking to this note.

Here are all the notes in this garden, along with their links, visualized as a graph.