Sample splitting is where you divide the dataset into two separate datasets, one acts as the training sample and one acts as the experimental sample. you test on and the other that you train on. You can just split your dataset randomly in half to accomplish this. However, in this case your variance results should be framed in terms of $n/2$ instead of $n$ since we have half of the sample. However, if you don’t like this loss of efficiency there is a solution to recover full sample size efficiency:

• after constructing the sample-split estimator, swap the samples, to use training as experimental and experimental as training, and then average the resulting estimators

Sample splitting is important because it prevents overfitting and allows for the use of arbitrarily complex estimators $\hat{\mu}_A(X)$

• Without sample splitting, one would have to restrict the complexity of the estimator $\hat{\mu}_A(X)$ via empirical process conditions (e.g., via Donsker class or entropy restrictions). Intuitively, this is because the estimator $\hat{\psi}$ is using the data twice: once to estimate the unknown function $\mu_A(X)$ and once to estimate the bias correction. Sample splitting ensures that these tasks are accomplished independently.

When is Doubly Robust Estimation Consistent (in Case of Observational Studies with unkown propensity and outcome estimators)

The classic advantage is that, when the nuisance functions $\pi$ and $\mu_A$ are estimated with parametric models, the doubly robust estimator is root-n consistent and asymptotically normal even if one of the two models is completely misspecified.

• In fact the doubly robust estimator has an even more useful advantage. Namely, it can be root-n consistent and asymptotically normal even when the nuisance functions π and μa are estimated flexibly at slower than root-n rates, in a wide variety of settings.

Kennedy proposes splitting sample into 3 separate groups:

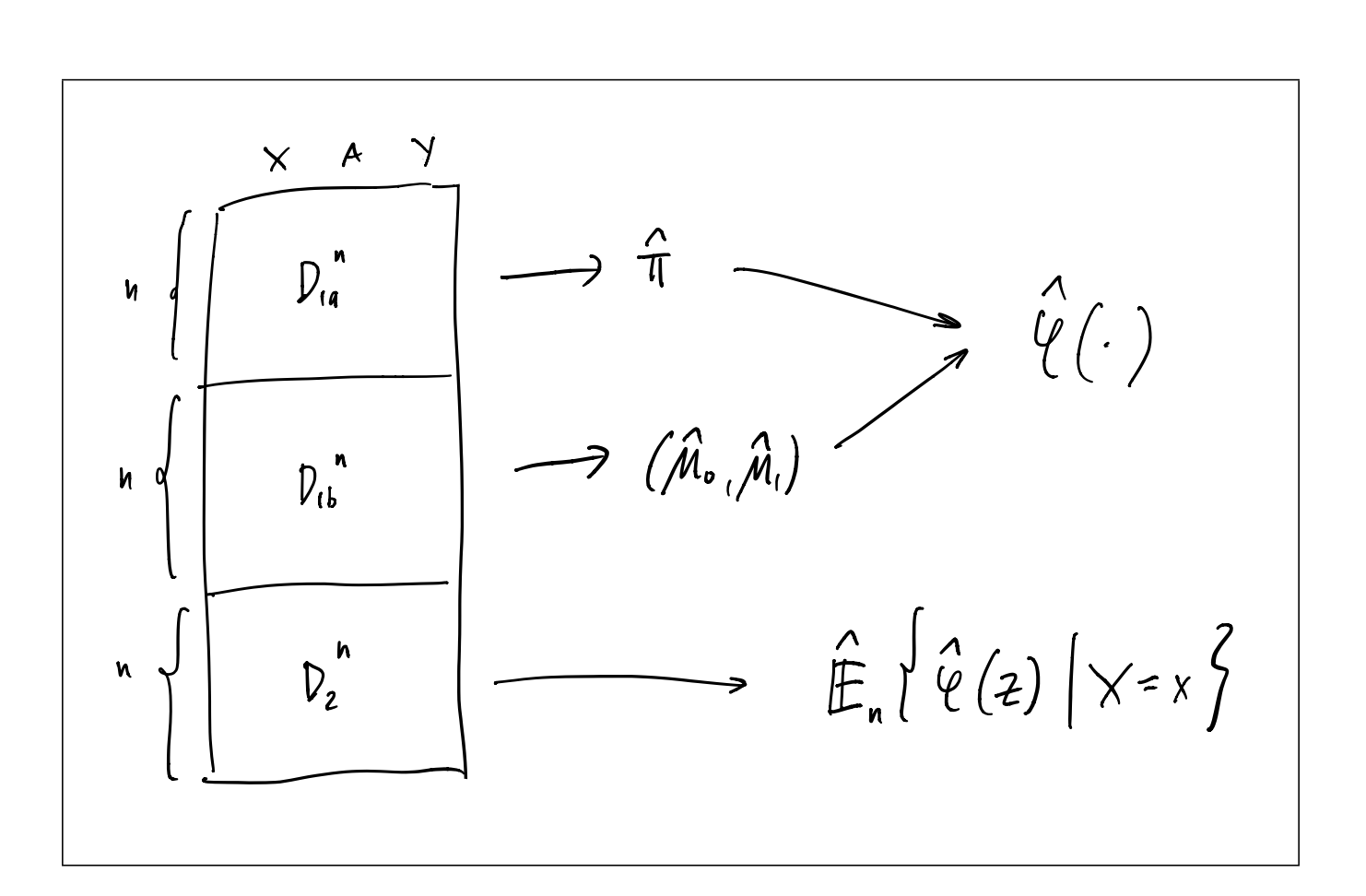
While the sample splitting procedure allows for less restrictive assumptions on the ML estimators, the sample splitting can introduce a new bias due to a specific sample. This can become more problematic the smaller the whole sample is. If we would have a sample with only 500 observations, 5-fold cross-fitting would use 400 observations for training and 100 for estimation. If we furthermore train each nuisance function with a different fold, we could only use 125 observations for training the doubly-robust estimator which include up to four different nuisance functions. To average any potential bias from sample-splitting we can repeat the estimation multiple times and take the mean or the median over all the estimators